Real-Time-Rendering-4 学习笔记

概述

最近研究Cesium框架，每每涉及到图形学底层相关的内容，就倍感吃力，所以想系统地把图形学的基础好好的夯实一下。
于是选择了Real-Time-Rendering-4作为学习图形学的入门书籍，目前是打算一个月左右先完整的过一遍，图形学博大精深，可不是一年两年就能学会的，目前也只是了解一些皮毛，对顶点/片源着色器，还有glsl有一些初步的了解。

图形渲染管线 (The Graphics Rendering Pipeline)

Anonymous —— “A chain is no stronger than its weakest link.”

佚名 —— “链条的坚固程度取决于它最薄弱的环节。”

渲染管线的核⼼功能就是利⽤给定的虚拟相机、三维物体、光源等信息，来⽣成或者渲染（render）⼀张⼆维图像。

类比流水线，但是整个流⽔线的效率会被执⾏速度最慢的那个阶段所影响

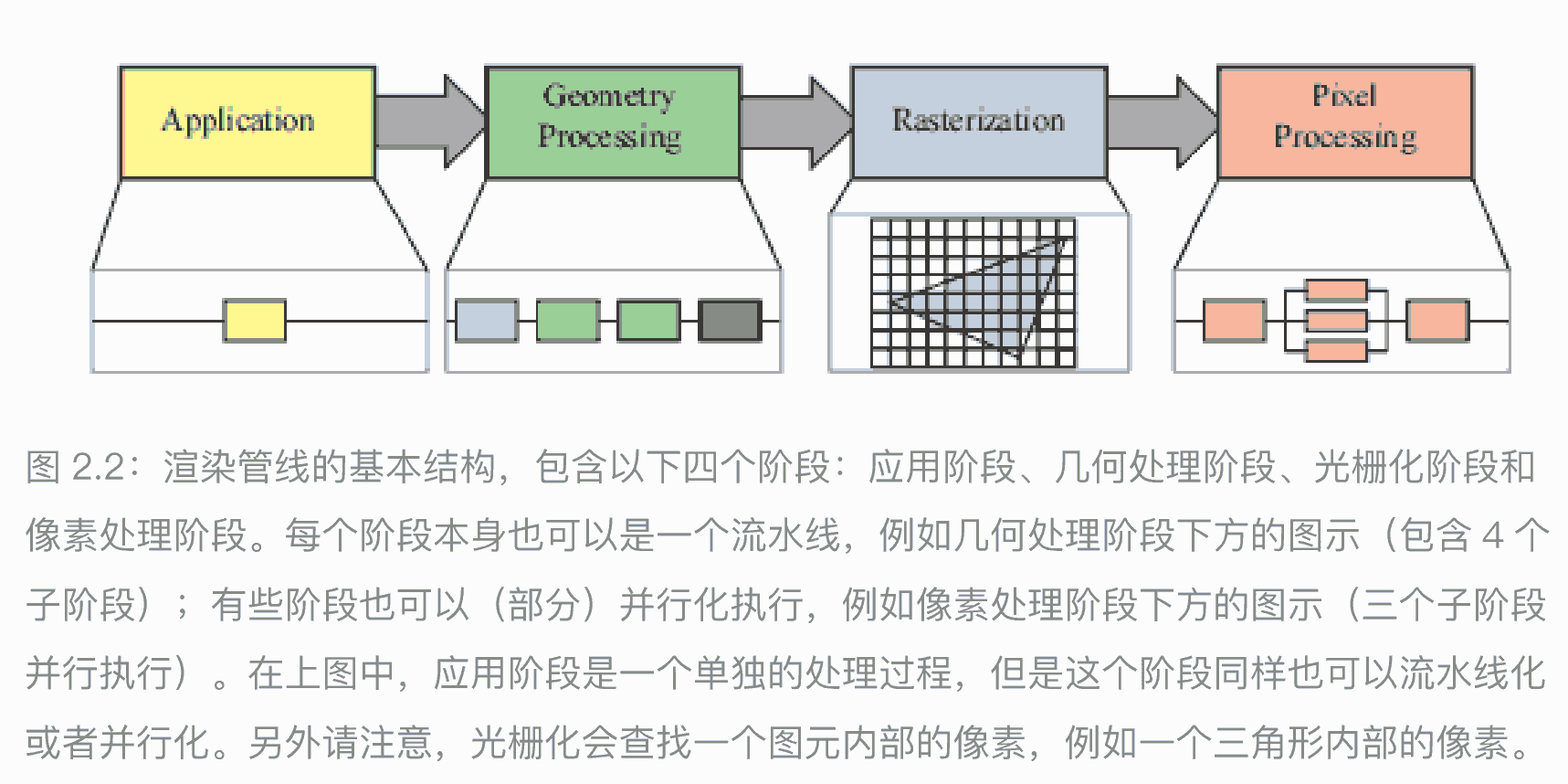
渲染管线的架构

1. 应用阶段 （application）
   运行在CPU，并行，⼀般CPU 会负责碰撞检测，全局加速算法，动画，物理模拟等任务
2. 几何处理阶段（geometry processing）
   运行在GPU，负责处理变换（transform），投影（projection）以及其他所有和⼏何处理相关的任务。这个阶段需要计算哪些物体会被绘制，应该如何进⾏绘制，以及应当在哪⾥绘制等问题。
3. 光栅化阶段（rasterization）
   运行在GPU，将构成⼀个三⻆形的三个顶点作为输⼊，找到所有位于三⻆形内部的像素，并将其转发到下⼀个阶段中。
4. 像素处理阶段（pixel processing）
   运行在GPU，决定每个像素的颜色，执行深度测试，判断像素是否可见

应用阶段 （application）

开发者可控制，修改程序，提高程序性能表现，如通过算法减少后续需要渲染的三角形数量。也可以通过计算着色器（compute shader）的独⽴模式，让GPU作为通用处理器来进行辅助计算。最后，要将需要渲染的集合物体输入到几何处理阶段。

碰撞检测，检测到碰撞后，产生相应的的响应，并返回给碰撞物体

处理其他来源的输入，如鼠标，键盘，头戴显示器等

几何处理阶段（geometry processing）

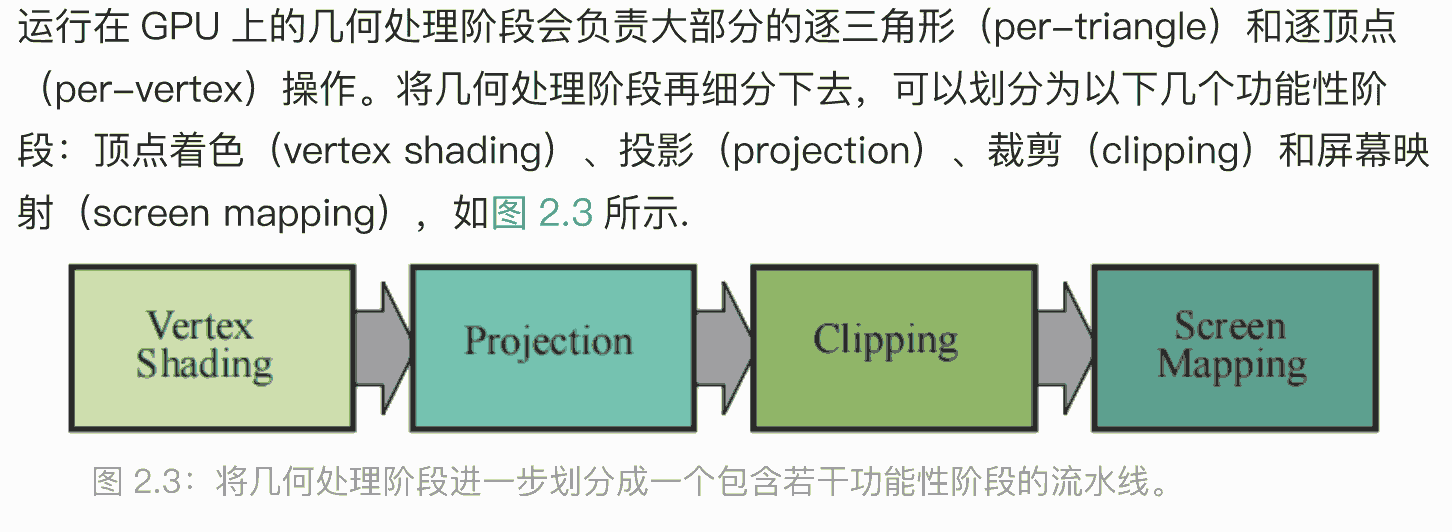
顶点着色

两个任务，1.计算顶点位置 2.计算开发人员想要输出的参数，如法线，纹理坐标
顶点位置计算过程

1. 模型坐标，即初始坐标，无任何变换，可以方便的调整自身位置和朝向等，目前的坐标系为模型坐标系
2. 模型坐标经过模型变换，得到了世界坐标，世界空间是唯一的，各个模型经过各自的模型变换后，所有的模型就位于同一个空间中，目前的坐标系为世界坐标系
3. 为了方便之后的投影操作和裁剪操作，世界坐标需要经过视图变换，得到视图坐标，其目的是为了将相机放在原点，并调整相机的朝向看向-Z，同时y轴指向上，x指向右，如此变换，形成相机空间（camera space），也可以叫做观察空间（view space），或者是眼睛空间（eye space），目前的坐标系为视图坐标系，也有人叫相机坐标系，眼睛坐标系
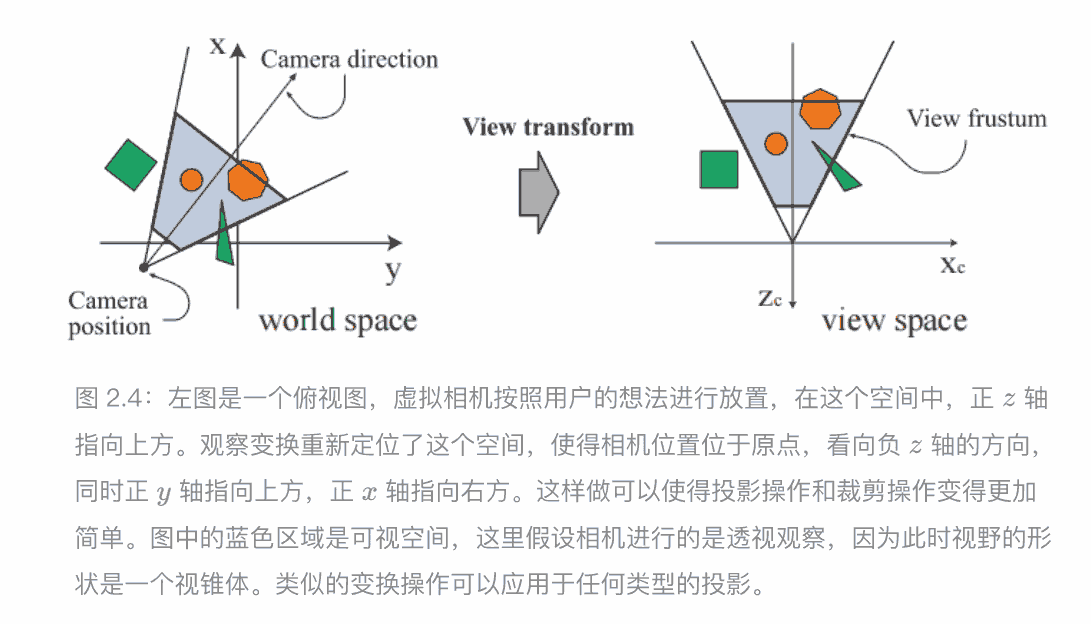
4. 通过投影矩阵将眼睛/视图/相机坐标，投影到裁剪空间（clipping space）中，有两种投影方法，正交投影，透视投影（近大远小），目前的坐标系为裁剪坐标系（clip coordinates）。坐标的z分量并不会被存储在⽣成的图像中，而是存储在⼀个叫做 z-buffer 的地方，通过这种⽅式，模型便从三维空间投影到了⼆维空间中。

顶点处理

完成顶点处理后，还有几个可以在GPU上执行的可选操作，顺序如下 曲⾯细分（tessellation）、⼏何着⾊（geometry shading）和流式输出（stream out）。是否使⽤这些可选操作，⼀⽅⾯取决于硬件的功能（并不是所有 GPU 都⽀持这些功能），另⼀⽅⾯取决于程序员的意愿。这些功能相互独⽴，⽽且⼀般并不是很常⽤

1. 曲面细分
   场景中的相机位置可以⽤来决定需要⽣成多少个三⻆形：当距离相机很近时，则⽣成较多数量的三⻆形；当距离相机很远时，则⽣成较少数量的三⻆形。
2. ⼏何着⾊器（geometry shader）
   ⼏何着⾊器有好⼏种⽤途，其中最流⾏的⼀种就是⽤来⽣成粒⼦。想象我们正在模拟⼀个烟花爆炸的过程，每颗⽕花都可以表示为⼀个点，即⼀个简单的顶点。⼏何着⾊器可以将每个顶点都转换成⼀个正⽅形（由两个三⻆形组成），这个正⽅形会始终⾯朝观察者，并且会占据若⼲个像素，这为我们提供了⼀个更加令⼈信服的图元来进⾏后续的着⾊。
3. 流式输出（stream out）
   这个阶段可以让我们把 GPU 作为⼀个⼏何引擎，我们可以选择将这些处理好的数据输⼊到⼀个缓冲区中，⽽不是将其直接输⼊到渲染管线的后续部分并直接输出到屏幕上，这些缓冲区中的数据可以被CPU 读回使⽤，也可以被 GPU 本身的后续步骤使⽤。

裁剪

在可视范围内的图元，才需要被发送到下一个阶段，光栅化，可视范围外的则不会被发送，对于一部分位于可是空间内部，一部分在外部的图元，需要进行裁剪操作，由于我们使用投影矩阵将可视空间变换为标准立方，所有图元都需要被标准立方体裁剪

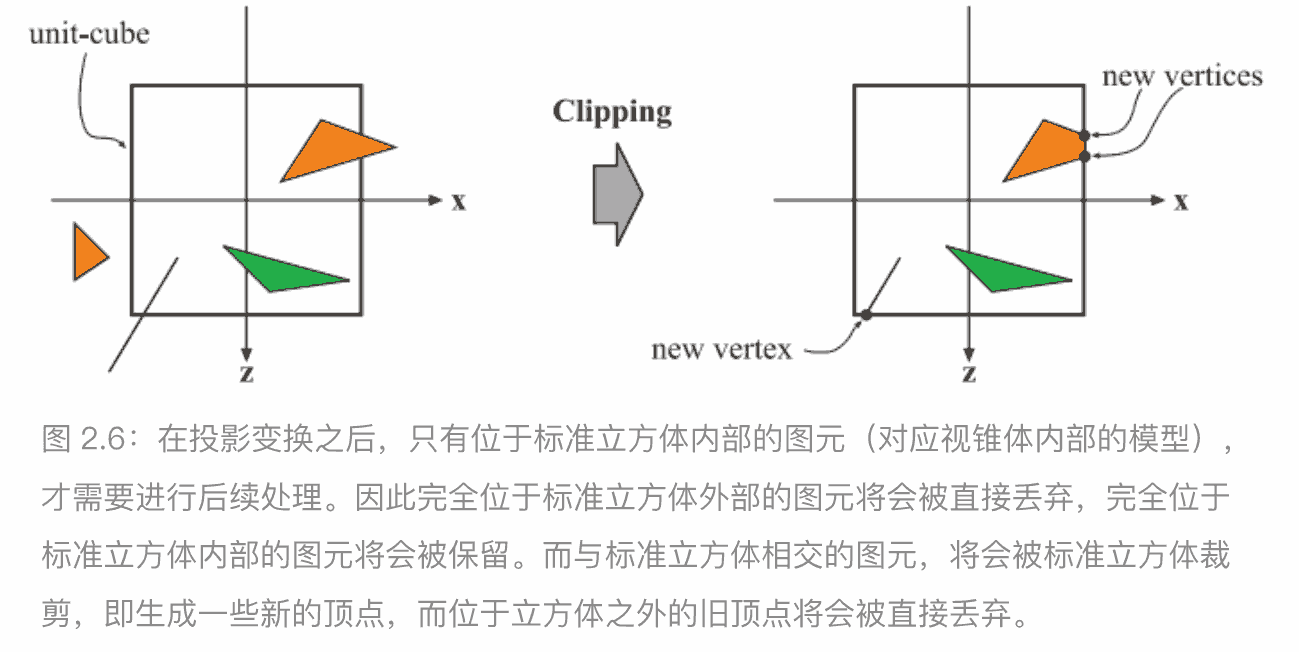
屏幕映射

光栅化阶段（rasterization）

光栅化也被称为扫描变换（scan conversion），这是⼀个将屏幕空间中⼆维顶点，转换到屏幕上像素的过程
可以使⽤点采样（point sample）来判定某个点是否位于三⻆形内部。最简单的⽅式就是直接将每个像素的中⼼点来作为该像素的样本，如果该像素的中⼼点位于三⻆形内部的话，那么我们就认为该像素也位于三⻆形的内部。我们还可以通过超采样（supersampling）或者多重采样抗锯⻮技术（multisampling antialiasing），来对每个像素进⾏多次采样
通过对三角形三个顶点的属性插值，获取每个三角形片元的属性

像素处理阶段（pixel processing）

像素着色

使用插值过的着⾊数据作为输入，来进⾏逐像素的着色计算，输出每个片元的颜色值，其中最重要的是纹理化

合并

将片元的颜色组合起来，这个阶段被称为ROP，光栅操作管线（raster operations pipeline）
该阶段还负责解决可见性问题，通过z-buffer（深度缓冲）实现，z-buffer存储每个像素的z值， 但不适用于透明物体的渲染

模板缓冲（stencil buffer）是⼀个离屏缓冲区（offscreen buffer），用来记录被渲染图元的位置信息

系统中的所有缓冲区在一起，被统称为帧缓冲（frame buffer）
屏幕上显示的内容就是颜色缓冲中的内容

图形处理单元 （The Graphics Processing Unit）-GPU

GPU 专注于⼀组⾼度并⾏化的任务，从⽽获得了很⾼的处理速度，它使⽤专⻔的硬件来实现 z-buffer，来能够快速访问纹理图像和其他缓冲区，还可以快速寻找哪些像素被⼀个三⻆形所覆盖

数据并行结构

遇到需要等待的指令，如读取纹理，gpu会切换到别的线程（warp），从而提高效率

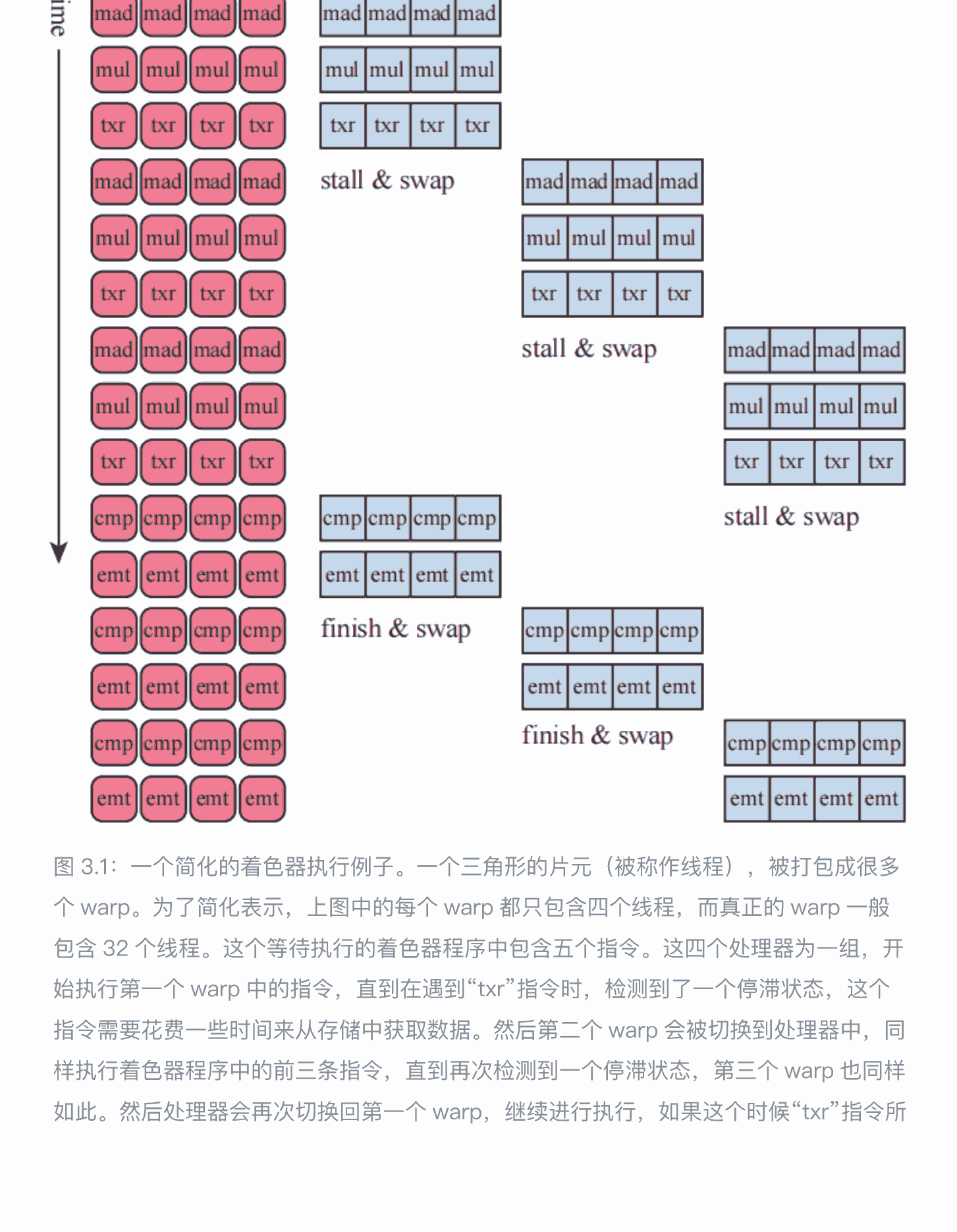
影响执⾏效率的另⼀个重要特征是着⾊器程序的结构，其中最重要的⼀个因素就是每个线程所使⽤的寄存器数量。我们现在假设 GPU 上可以同时存在两千个线程，每个线程中运⾏的着⾊器程序所需要使⽤的寄存器数量越多，那么 GPU 上能够同时存在的线程数量和 warp 数量也就越少。数量较少的 warp 意味着，可能⽆法通过 warp交换来缓解处理器核⼼的停滞，

另⼀个影响整体运⾏效率的因素是由“if”语句和循环语句导致的动态分⽀（dynamic branching）

GPU 管线概述

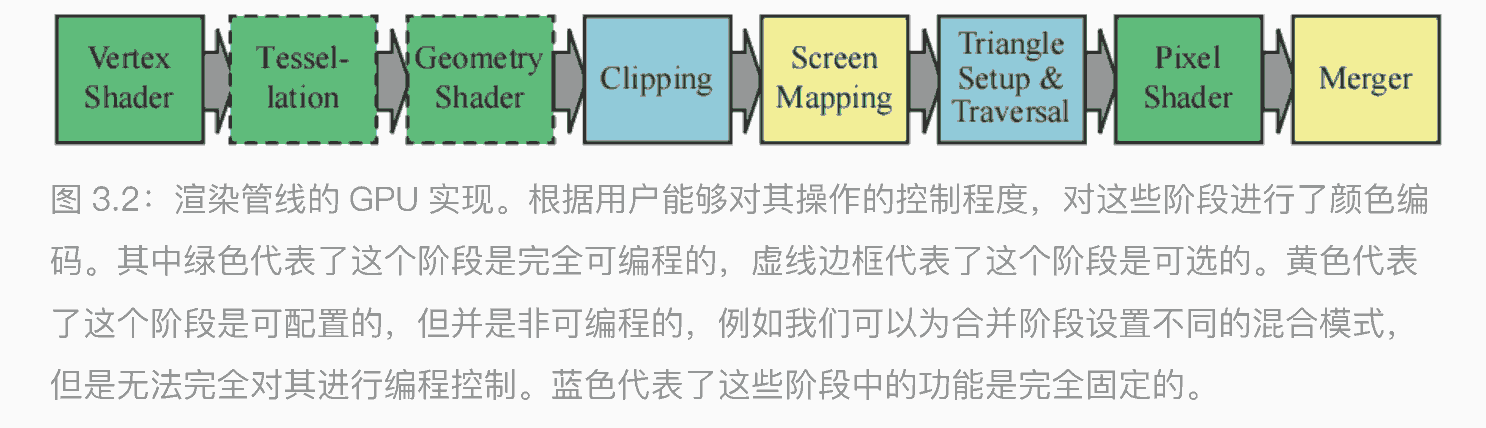
顶点着⾊器（vertex shader）是⼀个完全可编程的阶段，它⽤于实现渲染管线中的⼏何处理阶段。⼏何着⾊器（geometry shader）也是⼀个完全可编程的阶段，它可以对图元（点、线或者三⻆形）的顶点进⾏操作，它也可以⽤于进⾏⼀些逐图元的着⾊操作、销毁图元或者是创建新图元等。曲⾯细分（tessllation）阶段和⼏何着⾊器都是可选的阶段

裁剪、三⻆形设置和三⻆形遍历阶段，都由固定功能的硬件进⾏实现。屏幕映射受到窗⼝（window）和视⼝（viewport）设置的影响，其内部包含了⼀个简单的缩放和重定位功能。像素着⾊器阶段是⼀个完全可编程的阶段。合并阶段尽管不是可编程的，但是它是⾼度可配置的，我们可以为其设定各种各样的操作。合并阶段实现了渲染管线中的合并功能，负责修改维护颜⾊缓冲、z-buffer、混合、模板缓冲以及其他任何与输出相关的缓冲区。

可编程着色及其 API 的演变

⼀次 draw call 会调⽤图形 API 来绘制⼀组图元，渲染管线也会相应执⾏它所对应的着⾊器。每个可编程的着⾊器阶段都包含两种类型的输⼊：统⼀输⼊（uniforminput），它是指在⼀次 draw call 中不会发⽣改变的常量；可变输⼊（varyinginput），来⾃三⻆形的顶点或者光栅化的数据

发展历史

• NVIDIA 的Geforce256 是第⼀个被称作 GPU 的图形硬件，但是它仅仅只是可配置的，⽽不是可编程的。
• 2001 年初，NVIDIA 推出了 Geforce3 显卡，这是第⼀个⽀持可编程顶点着⾊器的GPU，它通过 DirectX 8.0 来暴露相关接⼝，并可以扩展到 OpenGL。
• 2002 年微软推出了包含 Shader Model 2.0 的 DirectX 9.0，它⽀持真正可编程的顶点着⾊器和像素着⾊器
• ⼤约在同⼀时间，OpenGL ARB（Architecture Review Board，架构审查委员会）也推出了 GLSL
• Shader Model 3.0 于 2004 年推出，并增加了动态流程控制，这使得着⾊器更加强⼤。它还将可选的功能特性纳⼊了需求列表，进⼀步扩⼤了可使⽤资源的范围，在顶点着⾊器中添加了对纹理读取的有限⽀持
• 2006 年底，DirectX 10.0 推出了 ShaderModel 4.0，它引⼊了⼏个重要特性，例如⼏何着⾊器和流式输出。
• 在 2009 年发布的 DirectX 11 和 Shader Model 5.0 中，增加了曲⾯细分着⾊器和计算着⾊器
• 图形 API 的下⼀个重⼤变化是由 AMD 于 2013 年提出的 Mantle API AMD 将⾃身 Mantle 的⼯作贡献给了 Khronos 组织，后者于 2016 年推出了新⼀代的 API，叫做 Vulkan。与 OpenGL ⼀样，Vulkan 可以⽤于多个操作系统。
• 在移动设备上⼀般会使⽤ OpenGL ES，其中“ES”代表的是嵌⼊式系统（embedded system）
• OpenGL ES 的⼀个分⽀是基于浏览器的 WebGL，它通过 JavaScripts 进⾏调⽤。它的第⼀个版本于 2011 年发布

顶点着色器

顶点着⾊器提供了⼀种⽤于修改、创建或者忽略三⻆形顶点数据的⽅法，这些数据可以是颜⾊、法线、纹理坐标和位置等。通常顶点着⾊器程序会将顶点从模型空间变换到⻬次裁剪空间中，在最极端的情况下，顶点着⾊器也必须要输出顶点的位置。
其他作用

• 物体⽣成：仅创建⼀次模型，并通过顶点着⾊器对其进⾏变形。
• 使⽤蒙⽪技术和变形技术来设置⻆⾊的身体动画和⾯部动画。
• 程序化变形：例如旗帜、布料和⽔⾯的运动。
• 粒⼦创建：通过向流⽔线发送简并（⽆⾯积）⽹格，并根据需要来设定它们的位置，从⽽来模拟粒⼦效果。
• 透镜畸变、热雾、⽔波纹、书⻚卷曲以及其他特效，可以通过将整个帧缓冲的内容作为⼀个纹理，然后将其应⽤在⼀个正在经历变形，并且屏幕对⻬的⽹格上进⾏实现。
• 通过使⽤顶点纹理来获取并应⽤地形的⾼度场

曲面细分阶段

曲⾯细分阶段允许我们绘制曲⾯，GPU 的任务就是将每个曲⾯描述都转换成⼀组三⻆形。
使⽤曲⾯细分阶段有⼏个好处。描述⼀个曲⾯往往要⽐提供三⻆形⽹格本身更加紧凑，除了节省内存之外，当场景中存在⼀些不断变化的⻆⾊或者物体时，这个功能还可以防⽌ CPU 与 GPU 之间的总线带宽成为程序的性能瓶颈。对于⼀个给定的相机视⻆，曲⾯细分可以⽣成适当的三⻆形数量，这样的曲⾯可以被⾼效渲染。

几何着色器

⼏何着⾊器可以将⼀种图元转换为另⼀种图元

像素着色器

在 OpenGL 中像素着⾊器被称为⽚元着⾊器（fragment shader）
多重渲染⽬标（multiple render target，MRT）
像素着⾊器并不会直接将⽣成的结果输出到颜⾊缓冲和 z-buffer 中，⽽是会为每个⽚元⽣成多组数值，并存储到不同的缓冲区中，每个缓冲区被称为⼀个渲染⽬标（render target，RT）
我们可以在⼀个 pass 中进⾏如下操作：在第⼀个渲染⽬标中⽣成颜⾊图像，在第⼆个渲染⽬标中⽣成对象标识符，并在第三个渲染⽬标中⽣成世界空间距离。MRT 的这种能⼒催⽣了⼀种不同类型的渲染管线，它被称作延迟着⾊（deferred shading），在延迟着⾊中，可⻅性计算和着⾊计算是在两个单独的 pass 中完成的

合并阶段

在合并阶段中，我们会将每个独⽴⽚元的颜⾊和深度进⾏组合，并最终形成帧缓冲。DirectX 将这个阶段叫做输出合并（output merger）；OpenGL 将其称为逐样本操作（per-sample operation）。
⽚元的深度值（以及其他任何可以使⽤的内容，例如模板缓冲或者裁剪测试，即 scissor）可以⽤于对可⻅性进⾏测试，不可⻅的⽚元将会被直接剔除，这个功能被称作为 early-z 使⽤ early-z 可以⼤⼤提升渲染管线的性能表现，详⻅章节 18.4.5

计算着⾊器

GPU 不仅可以⽤来实现传统的图形渲染管线，还可以⽤于很多⾮图形的领域，例如⽤于计算股票期权的估计价值，以及⽤于训练深度学习的神经⽹络等，这种使⽤硬件的⽅式叫做 GPU 计算（GPU computing）。
计算着⾊器的其中⼀个优势在于，它可以访问在 GPU 上⽣成的数据。由于在 GPU和 CPU 之间进⾏通讯是⼀件效率很低的事情，因此如果我们能够将数据驻留在 GPU上，并在 GPU 上进⾏计算，那么就可以⼤幅提⾼性能表现

Transform 变换

变换（transform）是指以点、向量、颜⾊等实体作为输⼊，并以某种⽅式对其进⾏转换的⼀种操作。

基本变换

平移

旋转

缩放

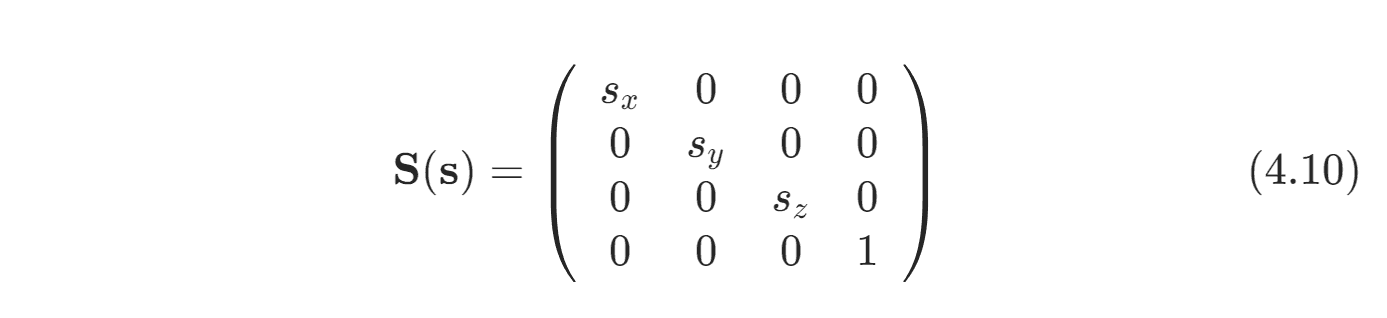
如果向量 中包含 1 个或者 3 个为负的分量，那么我们就获得了⼀个反射矩阵（reflection matrix）
⼀个顶点为逆时针顺序定义的三⻆形，在经过反射矩阵变换之后，其顶点顺序将会变成顺时针；顶点顺序的改变会导致错误的光照效果和背⾯剔除。我们可以通过计算左上⻆ ⾏列式的值，来判断⼀个给定的缩放矩阵是否为⼀个反射矩阵。如果缩放矩阵的⾏列式为负数，则说明该矩阵是⼀个反射矩阵

剪切矩阵

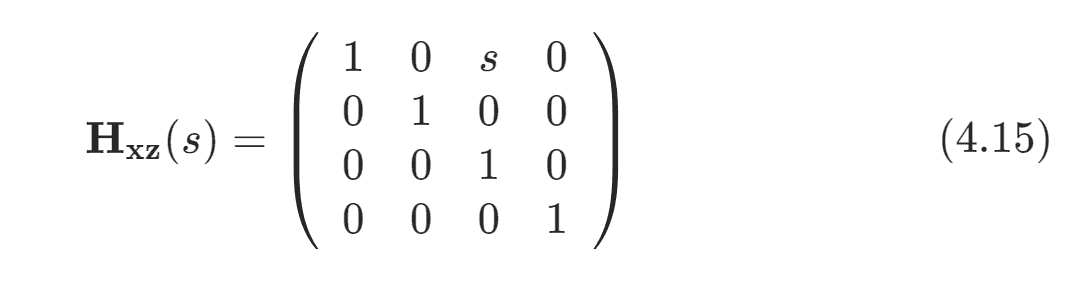
下标中的 （其索引为 0）代表了第 0 ⾏，下标中的 （其索引为 2）代表了第 2 列，因此我们可以知道参数 位于剪切矩阵的第 0 ⾏，第 2 列

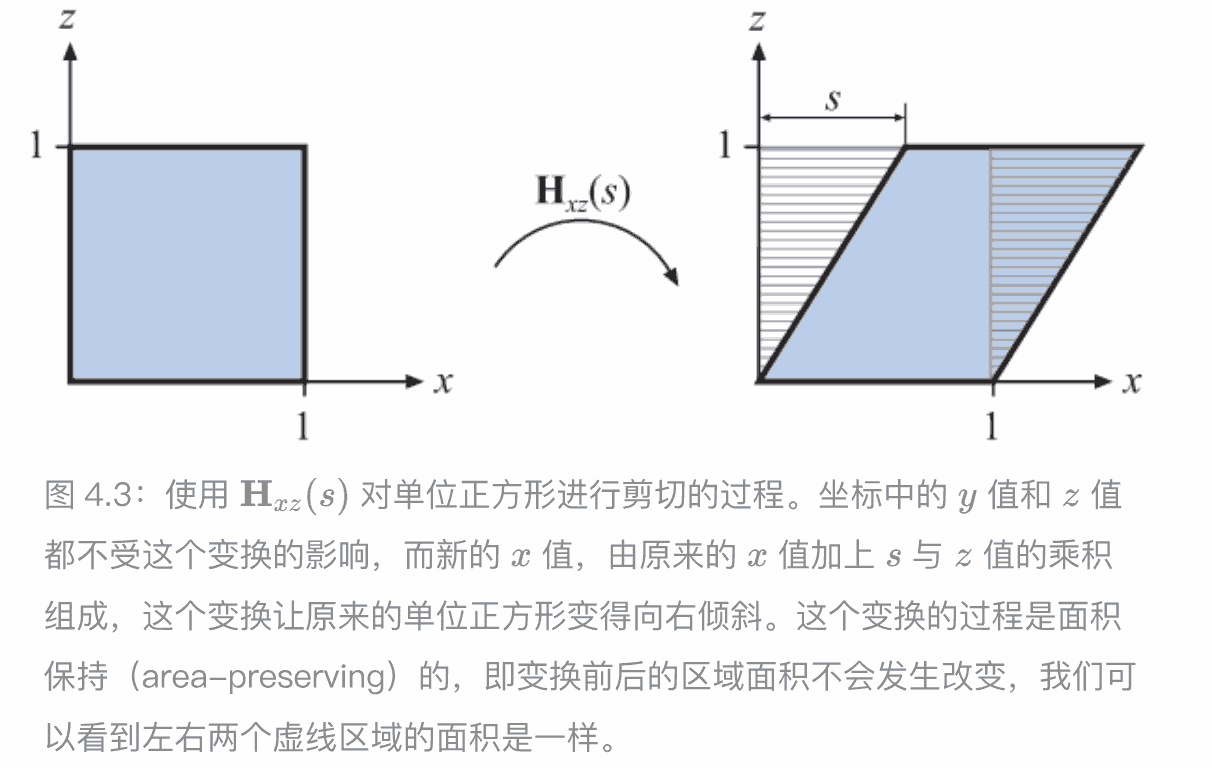
行列式不变,提及保持

刚体变换

在这个过程中，仅仅是物体的位置和朝向发⽣了变化，其形状和⼤⼩并没有受到任何影响。我们将这样只包含平移和旋转的变换叫做刚体变换（rigid-body transform），它具有保持⻓度、⻆度和⼿性的特点。
任何刚体变换矩阵 ，都可以写成⼀个平移矩阵 和⼀个旋转矩阵 的连接

法线变换

对法线正确的变换⽅法是：使⽤原始变换矩阵的伴随矩阵（adjoint）的转置矩阵来对其进⾏变换，⽽不是使⽤原始变换矩阵本身
矩阵的伴随矩阵是始终存在的。法线在经过变换之后，其⻓度可能会发⽣变化，因此在变换后通常还需要对法线进⾏归⼀化处理
法线变换的传统⽅法是，计算原始变换矩阵的逆矩阵的转置
如果变换矩阵完全由平移、旋转和均匀缩放（没有被拉伸或者压缩）操作组合⽽成的,可以直接使⽤模型的变换矩阵来对法线进⾏变换
还有⼀点需要注意⼀下，如果表⾯法线是从变换之后的三⻆形中计算出来的话（例如使⽤三⻆形的边向量进⾏叉乘，从⽽获得垂直于三⻆形表⾯的法线），那么法线变换的问题就不需要进⾏考虑了。切向量的本质和法线并不相同，它可以直接使⽤原始变换矩阵进⾏变换。

求逆矩阵

特殊变换

欧拉变换

欧拉变换可以构建⼀个旋转矩阵，将我们⾃身（相机）或者其他物体指向⼀个特定的⽅向

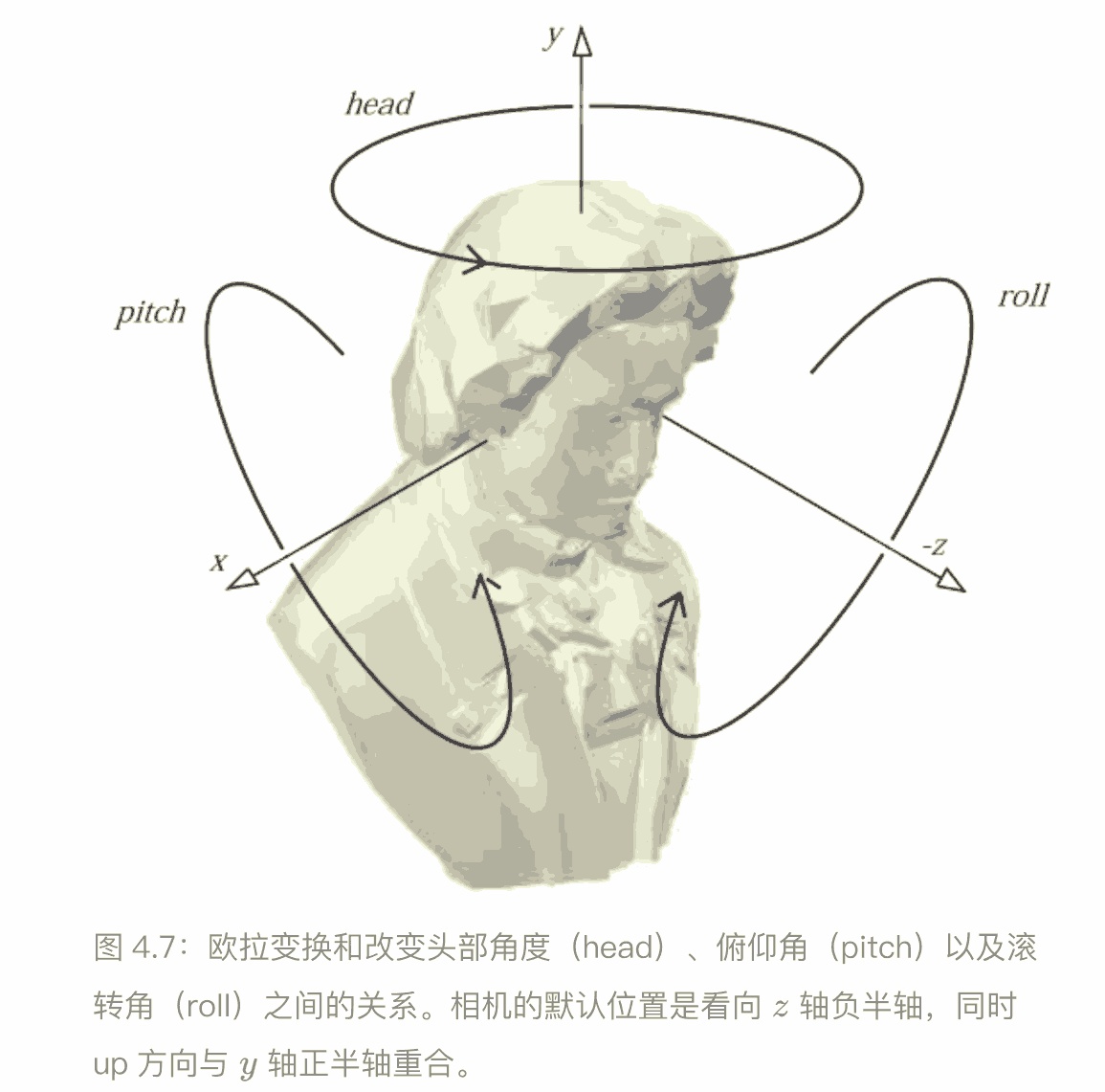
欧拉变换是三个旋转矩阵相乘的结果,所以其本身也是一个正交矩阵,
的欧拉⻆参数 代表了每个⽅向（head 头部，pitch 俯仰⻆，roll 滚转⻆）上绕轴旋转的⻆度
欧拉⻆在⼩⻆度变换和调整观察者⽅向⽅⾯⼗分有⽤，但是它也有⼀些严重的限制，即我们很难将两组欧拉⻆组合在⼀起,这也是使⽤其他⽅向表示⽅法（例如四元数）的原因之⼀
使⽤欧拉⻆也会导致⼀个叫做万向节死锁（gimbal lock）的问题

从欧拉变换中提取参数

在某些情况下，我们需要从⼀个代表欧拉变换的矩阵中，提取出各个⽅向上所改变的参数 h,p,r，即欧拉变换的参数

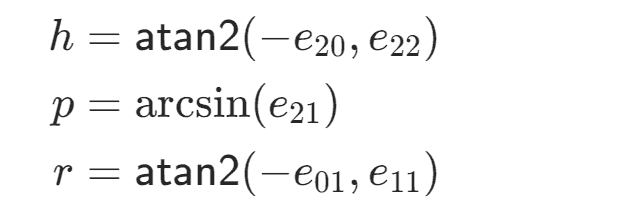
但是，这⾥我们还需要处理⼀种特殊情况，即当 cos p = 0 的时候，我们会遇到被称为万向节死锁的问题, 此时旋转⻆度 r,h 将会围绕着同⼀个旋转轴进⾏旋转
通过计算 r = atan2(-e10,e00), 还有一点 由于arcsin的定义域是 -π/2 <= p <= π/2，如果我们的p在这个范围外来创建变换矩阵E的话,我们将无法通过E计算出最初的p值,对于同一个E,hpr的组合并不是唯一的

矩阵分解

刚刚我们就从正交矩阵中,提取出了欧拉角
从⼀个变换矩阵中提取出平移矩阵是很简单的，我们只需要找到 矩阵中的最后⼀列元素即可。我们还可以对变换矩阵的⾏列式进⾏检查，如果⾏列式的值是⼀个负数，那么就说明这个矩阵包含⼀个反射变换。⽽想要分离出旋转、缩放和剪切变换则需要更多的的努⼒。

绕任意轴旋转

四元数

四元数可以⽤于表示旋转和⽅向，它在很多地⽅都⽐欧拉⻆和矩阵表示更加优秀。任何三维⽅向都可以表示为⼀个绕特定轴的简单旋转，给定⼀个旋转轴和旋转⻆度，我们可以直接将其转换为⼀个四元数，或者是从⼀个四元数中提取出旋转轴和旋转⻆度；但是对任意⽅向上的欧拉⻆进⾏转换是很困难的。四元数可以⽤于稳定且恒定速度的⽅向插值，这是欧拉⻆很难实现的。
复数由⼀个实部和⼀个虚部组成，每个复数都可以使⽤两个实数进⾏表示，其中第⼆个实数要乘以 √-1。
类似地，四元数由四个部分组成，前三个值与旋转的轴有关，⽽旋转⻆度会对四个值都产⽣影响

四元数的数学背景

目前理解不了…pass
https://eater.net/quaternions 可视化四元数网站

四元数变换

单位四元数（unit quaternion），它们的模⻓为 1。单位四元数可以⽤于表示任何的三维旋转，⽽且这种表示⽅式⾮常紧凑和简单。

球面线性插值

顶点混合

顶点混合（vertex blending）是⼀种解决类似两段机械手臂,解决关节灵活柔韧的问题的常见方法. 它还有⼏个其他的名称，例如：线性蒙⽪混合（linear-blend skinning）、包络（enveloping）或者⻣架⼦空间变形（skeleton-subspace deformation）

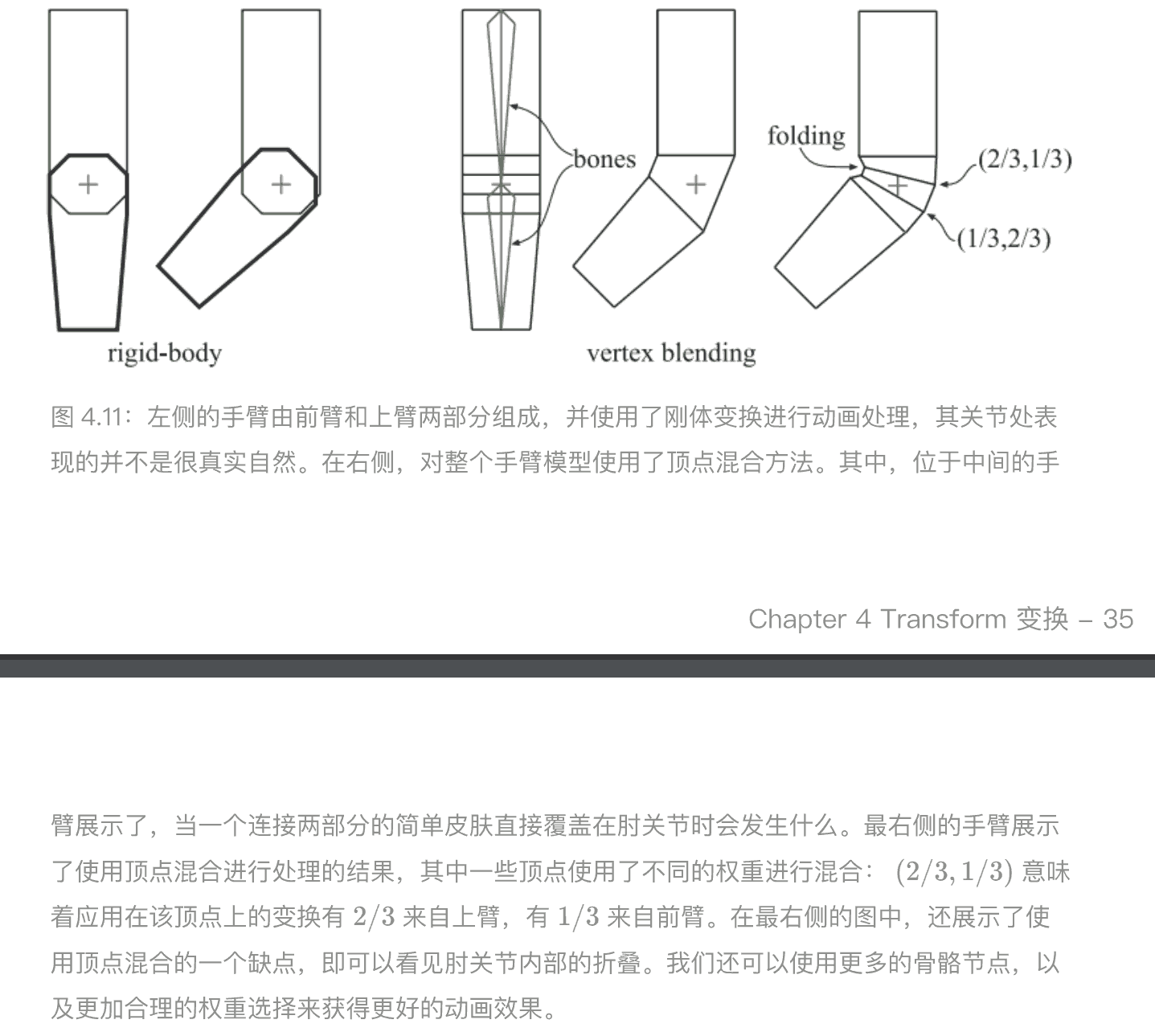
最基础的顶点混合算法，它当然会存在⼀些缺点，例如我们不希望出现的折叠、扭曲或者是⾃相交等现象
更好的⽅案是使⽤双四元数混合（dual quaternion）,这个技术可以让蒙⽪保持原始形状的刚性，从⽽避免四肢出现像“糖纸”⼀样的扭曲

变形

在动画中，从⼀个三维模型变形到另⼀个三维模型是⾮常有⽤的

几何缓存回放

在⼀些过场动画中，我们可能会希望使⽤⼀些极⾼质量的动画，这些⾼质量动画使⽤上述我们所提到的任何⽅法和技术都⽆法实时实现。⼀种简单的⽅法是，将所有帧的顶点数据预先计算并存储起来， 然后在游戏运⾏的时候，从磁盘上读取这些数据并对顶点进⾏更新。但是对于⼀个包含 30000 个顶点的模型⽽⾔，⼀段简单的动画可能就会占据 50 MB/s 的带宽。Gneiting 提供了若⼲种⽅法，可以将内存消耗降低到原来的 10%

投影

在真正渲染⼀个场景之前，场景中所有的相关物体都需要被投影到某个平⾯上，或者是某个简单空间中。在投影变换完成之后，才会进⾏裁剪操作和渲染操作

正交投影

当使⽤正交投影来观察⼀个场景的时候，⽆论场景中的物体距离相机多远，它们的⼤⼩都不会发⽣改变

由于行列式为0, 所以不可逆,即我们将⼀个物体从三维空间变换到⼆维平⾯上，是没有办法将丢失的维度信息恢复的

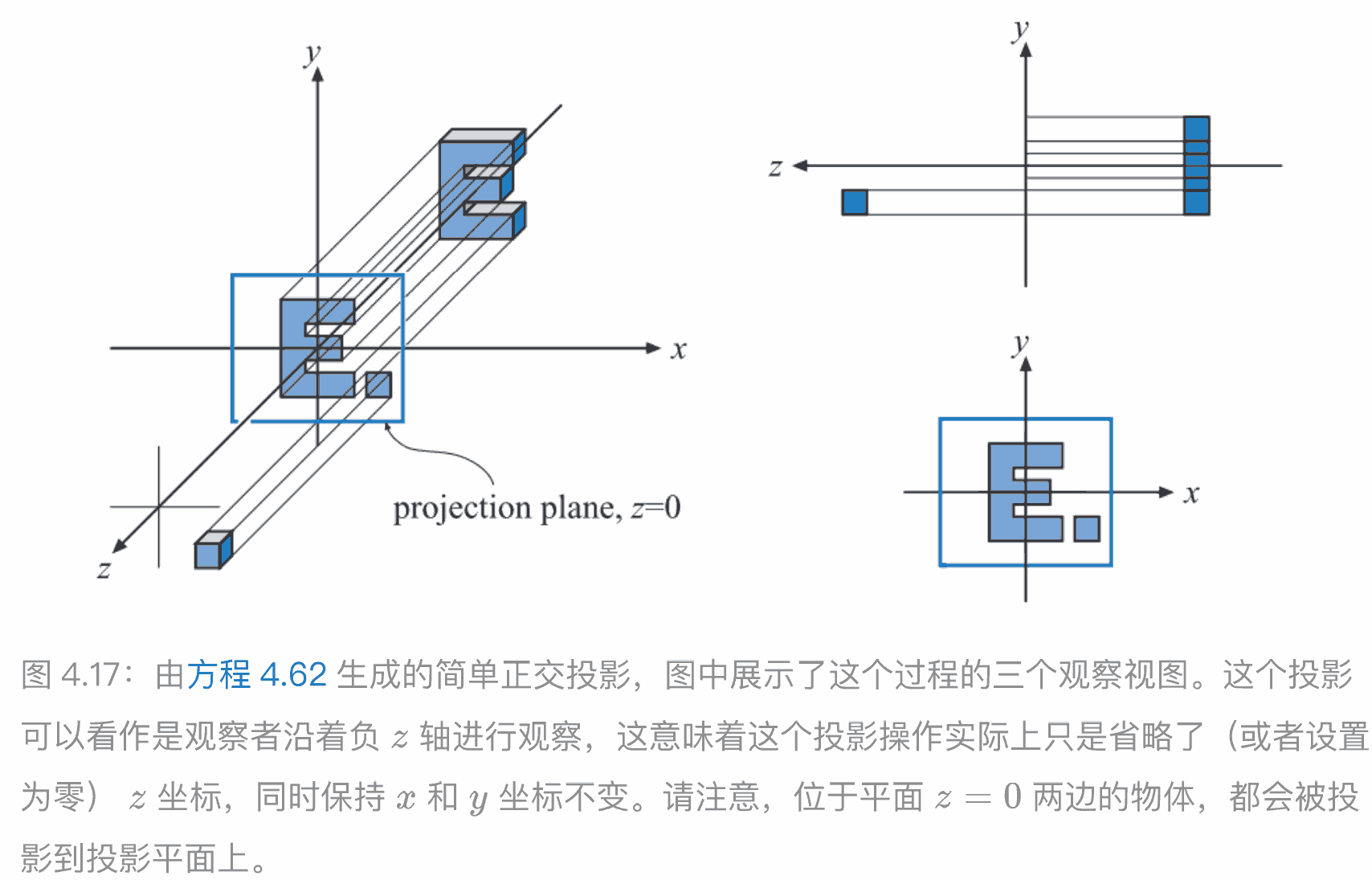
通常我们会使⽤⼀个六元组（l,r,b,t,n,f ）来描述⼀个正交投影矩阵，它们分别代表了左侧、右侧、底部、顶部、近裁剪平⾯以及远裁剪平⾯。这个矩阵会将代表可视空间的轴对⻬包围盒（axis-aligned bounding box)，简称 AABB

透视投影

透视投影更加符合我们⼈眼观察这个世界的模式，因为它具有近⼤远⼩的特点
与正交投影类似，透视投影并没有真正地将所有物体都投影到了⼀个平⾯上（这个过程是不可逆的），⽽是将视锥体变换成了⼀个规则观察体

视场⻆（field of view，FOV）是提供场景感的重要因素，与电脑屏幕相⽐，眼睛本身就有⼀个物理上的视场⻆（⼈类单眼的⽔平视场⻆最⼤可达 156 度，双眼的⽔平视场⻆最⼤可达 188 度；⼈类两眼的重合视场⻆为 124 度，单眼的舒适视场⻆为 60度；当集中注意⼒时，视场⻆约为 25 度。）
如果使⽤⽐⼈眼物理视场⻆更⼩的视场⻆，会减弱透视的感觉，因为观察者在场景中的视野会被放⼤；如果使⽤⼀个更⼤的视场⻆的话，会使得场景中的物体看起来很扭曲（例如使⽤相机的⼴⻆镜头），尤其是在靠近屏幕边缘的地⽅，会夸⼤近距离物体的⽐例。然⽽，视场⻆越⼤，意味着视野越⼴阔，可以让观察者感觉看到的物体更⼤，更加令⼈印象深刻；其优势在于可以为⽤户提供更多的环境信息。

着色基础 Shading Basics

着色模型

模型⽤于描述物体的颜⾊是如何随着表⾯朝向、观察⽅向和光照等因素的变化⽽变化的。

Gooch 着⾊模型的基本思想是⽐较表⾯法线和光源的位置：如果法线直接指向了光源，那么就会使⽤⼀种暖⾊调来给表⾯着⾊；如果法线没有指向光源，则会使⽤⼀种冷⾊调来给表⾯着⾊；如果法线位于这两个状态之间，则会在冷暖⾊调之间进⾏插值

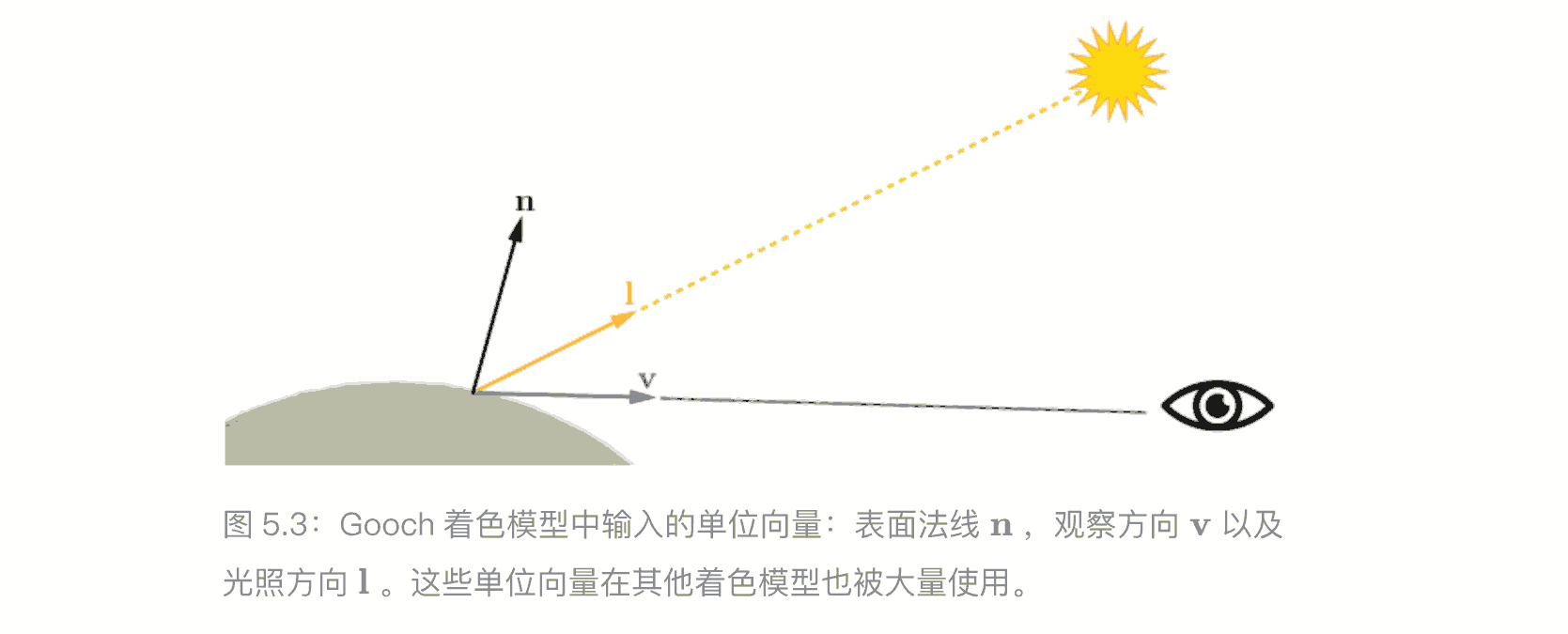
常见线性插值操作,t*Ca + (1 - t)Cb t属于 0到1, t在0-1变化时, 最终结果会在Ca和Cb中插值,获得颜色, 一般着色器都会提供内置插值函数,如lerp或者mix

光源

现实世界中的光照是⾮常复杂的，可能会有很多个光源，每个光源的⼤⼩、形状、颜⾊以及强度都可能会不相同；⽽间接光照的情况就更加复杂了
⼀个光源可以通过两个关键参数来与着⾊模型进⾏相互作⽤：指向光源的光线⽅向 L ，以及光线的颜⾊ light

方向光

是光源模型中最简单的⼀个， 光线方向和颜色是固定的，，当场景到光源的距离相对于场景尺⼨⽽⾔很⼤的时候，⽅向光的效果会很好。

精确光源（点光源）

光照强度随着距离衰减， 即 光照颜色 = 初始颜色 * （参考距离/光照距离）^2 但有两个问题，如果距离过小，光照强度就会趋于无限大，通常会给分母加一个较小的数, 还有一个问题就是很远的地方,我们期望光照的范围为20米,超过这个距离后则不会应用光照,并且边缘处不能尖锐截断,通常会使用窗函数来解决

聚光灯

与点光源不同的是，现实世界中⼏乎所有光源的光照，不仅会随着距离的改变⽽发⽣变化，同样也会随着⽅向的改变⽽发⽣变化

实现着色模型

为了在实际中进⾏应⽤，这些着⾊⽅程和光照⽅程必须要在代码中进⾏实现,有以下几点需要在编写代码时考虑

计算频率

当设计⼀个着⾊实现的时候，我们需要评估它的计算频率（frequency of evaluation）
如果计算的结果是一个常数,固定的值,那么可以在cpu中提前计算完成
另⼀种情况是，⼀个着⾊计算的结果会在应⽤程序运⾏的过程中发⽣变化，但是其变化的频率很慢，因此并不需要每⼀帧都进⾏更新

需要注意的是，即使顶点着⾊器总是会输出单位⻓度的的表⾯法线，但是光栅化插值也可能会改变它们的⻓度,对于表面法线,通常会在顶点着色器和像素着色器中都进行归一化

与表⾯法线不同，指向特定位置的向量（例如观察向量和光线向量），通常并不会进⾏插值

实现示例

glsl中,输入输出的变量用in 和 out标记 像素着⾊器的输⼊与顶点着⾊器的输出是相匹配的

in vec3 vPos;
in vec3 vNormal;
out vec4 outColor;

统一值,定义点光源

struct Light {
   vec4 position;
   vec4 color;
}

uniform LightUBlock {
   Light uLights [ 2 ];
}
uniform uint uLightCount;

像素着色器

vec3 lit (vec3 l, vec3 n, vec3 v){
   vec3 r_l = reflect(-l, n);
   float s = clamp(100. * dot(r_l,v) - 97.0, 0.0, 1.0);
   vec highlightColor = vec3(2,2,2);
   return mix (uWarmColor, highlightColor, s)
}

材质系统

最常⻅的情况就是参数化材质，在最简单形式中，材质参数化需要两种材质实体：材质模板（material template）和材质实例（material instance）

锯齿(走样)和抗锯齿(反走样)

⼀旦⽹格单元的中⼼被三⻆形所覆盖，这个单元的像素颜⾊就会⽴即从⽩⾊变为⿊⾊。三⻆形会以像素的形式显示出来，⼀个⽹格像素要么被覆盖，要么不被覆盖，绘制出来的线也有类似的问题. 由于这个原因，因此三⻆形和线段的边界会呈现出锯⻮状

采样和滤波理论

渲染图像的过程本质上是⼀个采样任务。这是因为图像的⽣成实际上就是对三维场景进⾏采样的过程，从⽽获得图像（离散像素数组）中每个像素的颜⾊值
当⼀个信号的采样率过低时，就会出现⾛样现象（在光栅化游戏中，屏幕的分辨率⼤体决定了采样率，因此屏幕分辨率越⾼，⾛样和锯⻮现象就越少）。

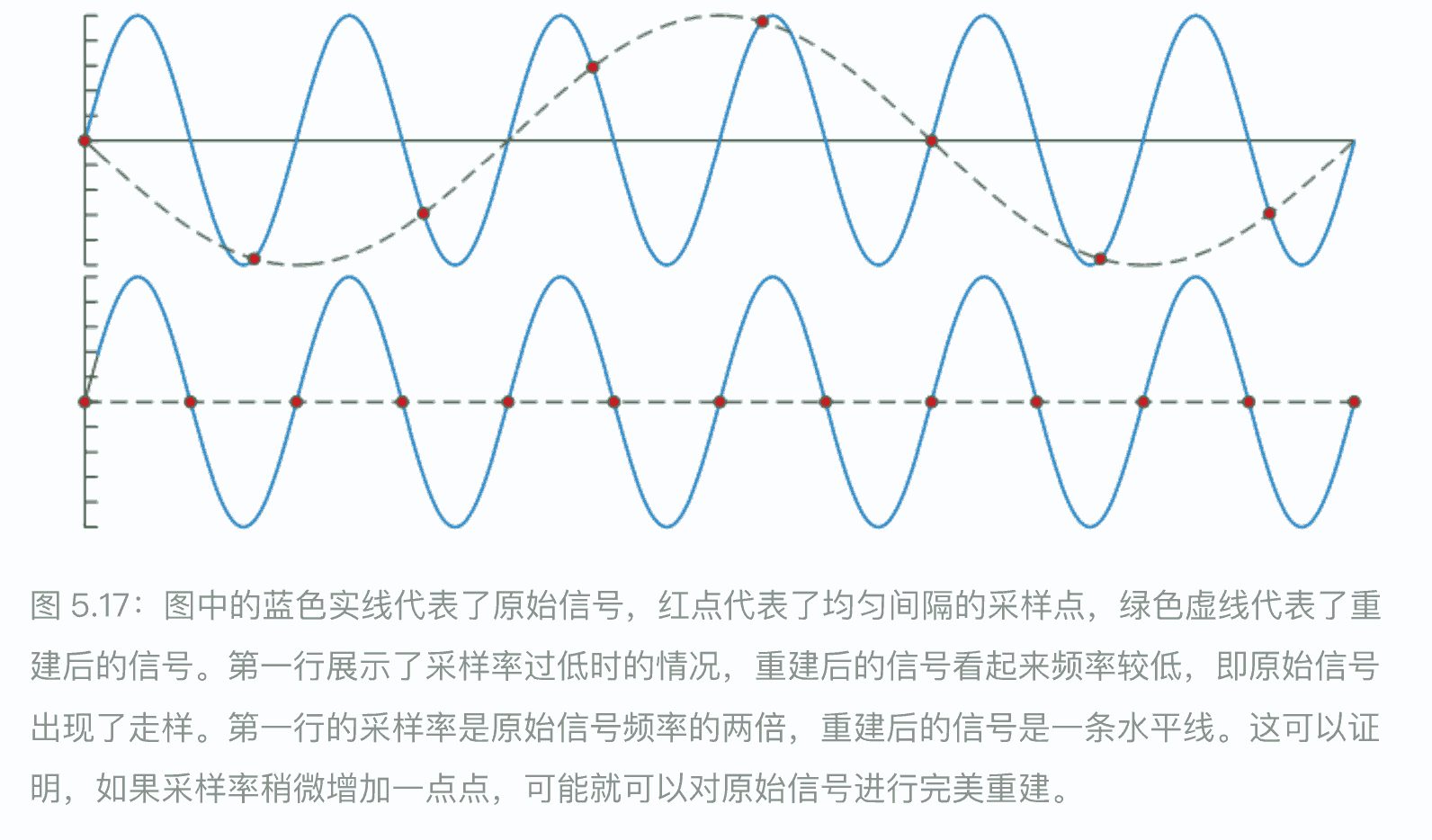
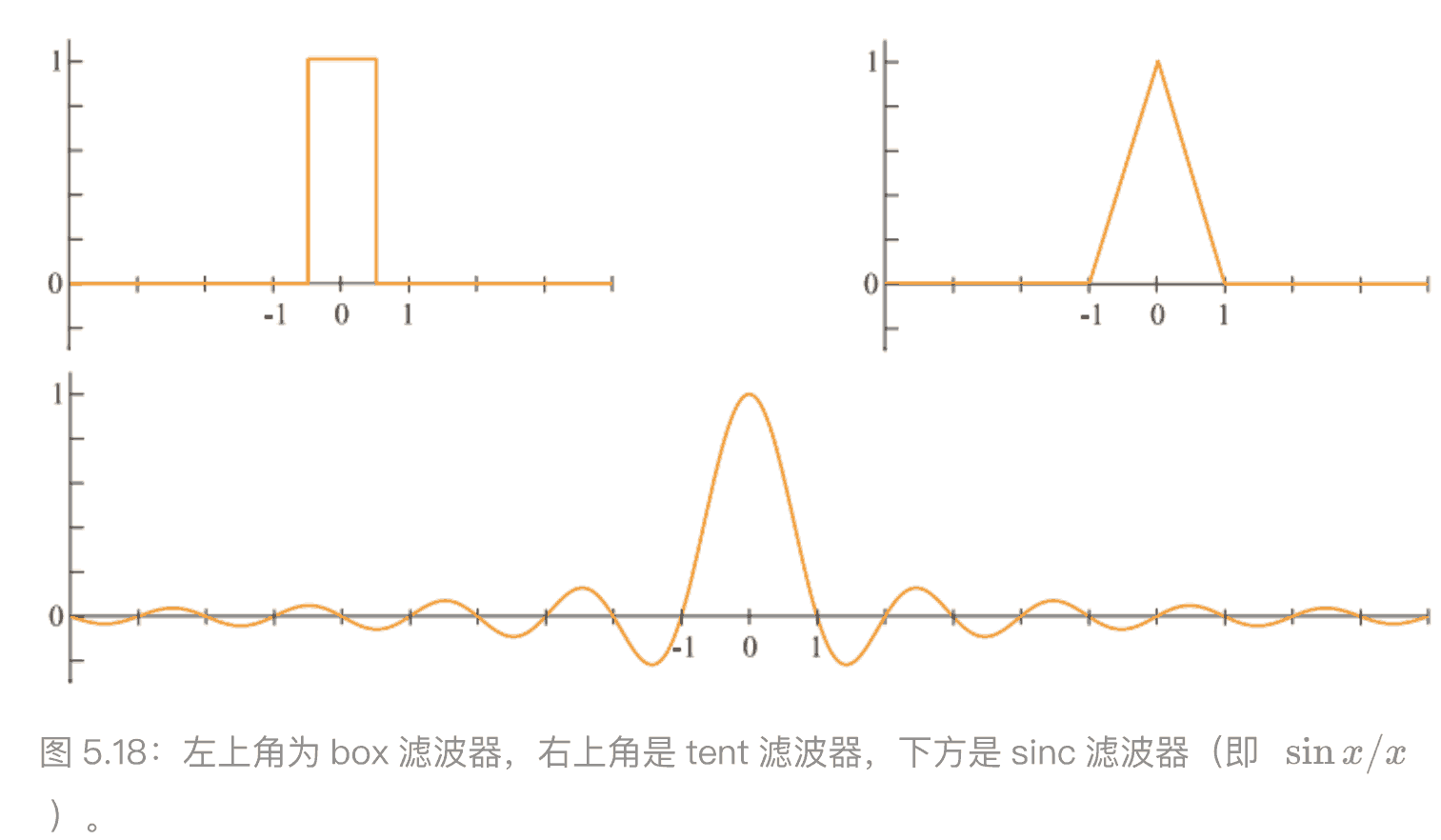
重建

给定⼀个有限频宽的采样信号后，现在我们将讨论如何从采样信号中重建原始信号。为了实现这个⽬的，我们必须使⽤⼀个滤波器,这⾥需要注意的是，滤波函数的积分⾯积应当始终为 1，否则重建后的信号就会被放⼤或者缩⼩。